
The Zero-Knowledge Proof (ZKP) was first introduced in 1985 by S. Goldwasser, S. Micali, and C. Rackoff. With the rise of ZK-Rollups in 2022, it has become a crucial tool for Ethereum scalability. ZKP mathematically solves the problem of proving the correctness of statements while keeping the knowledge hidden. It can be used in various scenarios that demand privacy and security, such as self-identity and rights authentication, without revealing private information.
It falls under the category of privacy security, and when combined with blockchain, it is mainly used for private transactions (e.g., zcash and tornado.cash). However, with the advent of web3, ZKP has become one of the cornerstones of the technology due to its efficient compression and verification capabilities in decentralized data verification, multi-chain interoperability transactions, and layer2 transactions.
Numen will publish a six-part series on the Introduction to Zero-Knowledge Proof to help everyone better understand the concept. This first article will cover the background, definition, and related concepts of ZKP.
Preface
In 2021, the Abel Prize was awarded to two prominent figures in mathematics and computing: Hungarian mathematician László Lovász and Israeli computer scientist Avi Wigderson.

László Lovász’s main contributions:
- LLL algorithm (with the Lenstra brothers)
- Graph theory (color filling problem)
Avi Wigderson’s main contributions:
- Proving that “if an algorithm with randomness appears to be efficient, then there must be an equally efficient non-random algorithm.”
- Demonstrating that essentially all NP problems can be rewritten for use with “zero-knowledge proof.” Wigderson’s research established the theoretical foundation for zero-knowledge proof [1]
Zero-knowledge proof were first proposed by S. Goldwasser, S. Micali, and C. Rackoff in 1985 [2]. However, after Wigderson laid the theoretical foundation in 1991, it wasn’t until 2010 that the field began to rapidly develop.
Initially, zero-knowledge proof were merely mathematical concepts with no real-world applications or methodology. However, the rise of blockchain technology and the development of Groth’s methodologies have provided practical applications and a framework for their use.
1. Popular Understanding of Zero-Knowledge Proof
Official definition: Zero-knowledge proof is a method where a prover can convince a verifier that a specific assertion is correct without revealing any additional information to the verifier.
Example 1: Blind Ball Test
Alice is colorblind, Bob is not colorblind. Alice has two balls of identical size and shape but different colors, and Bob needs to prove to Alice that the two balls are not the same color. In this scenario, Alice is the verifier and must verify Bob’s statement, while Bob is the prover and must prove that the two balls are different colors.
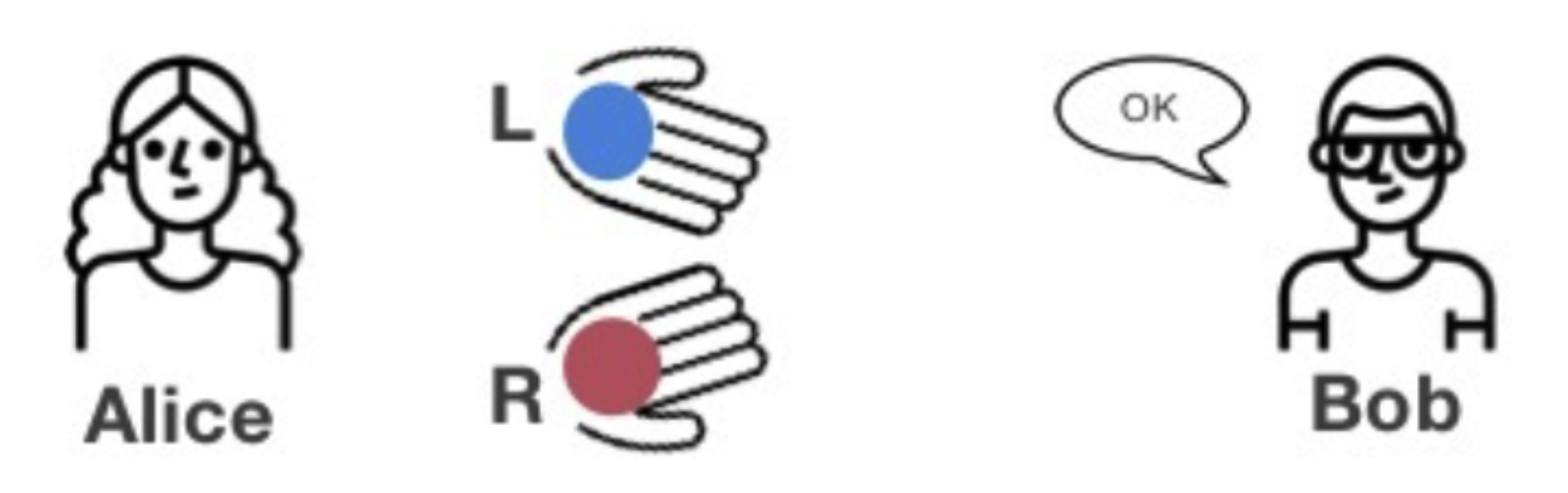
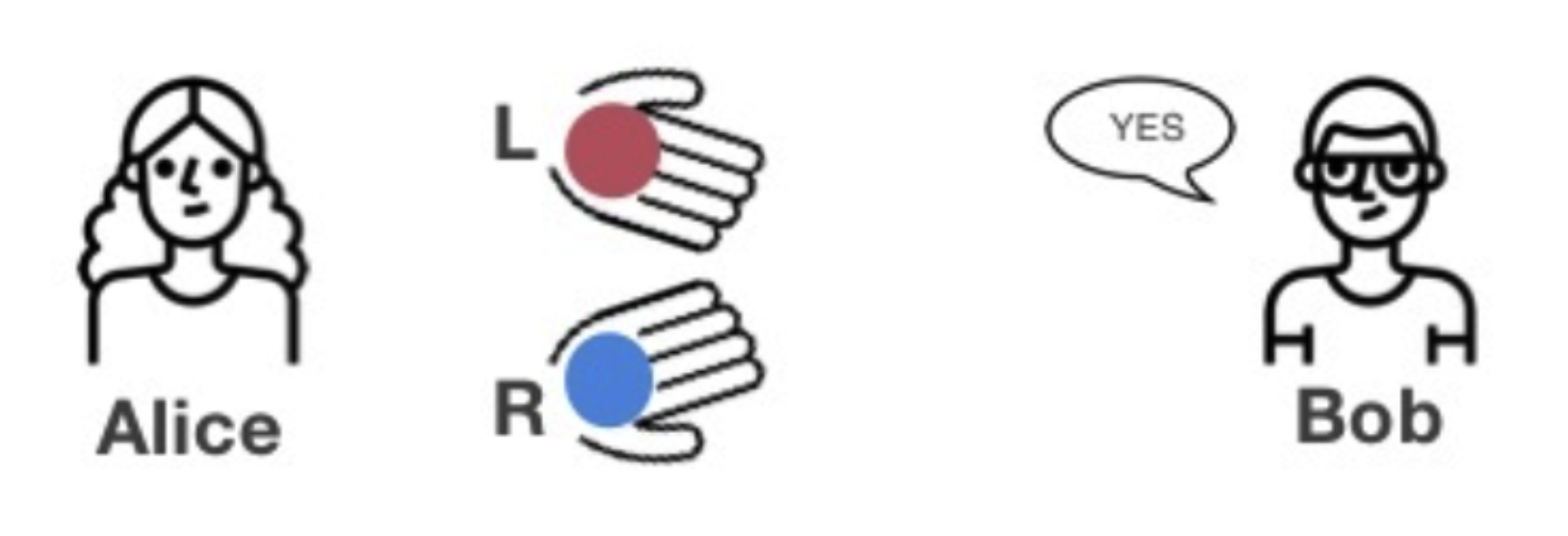
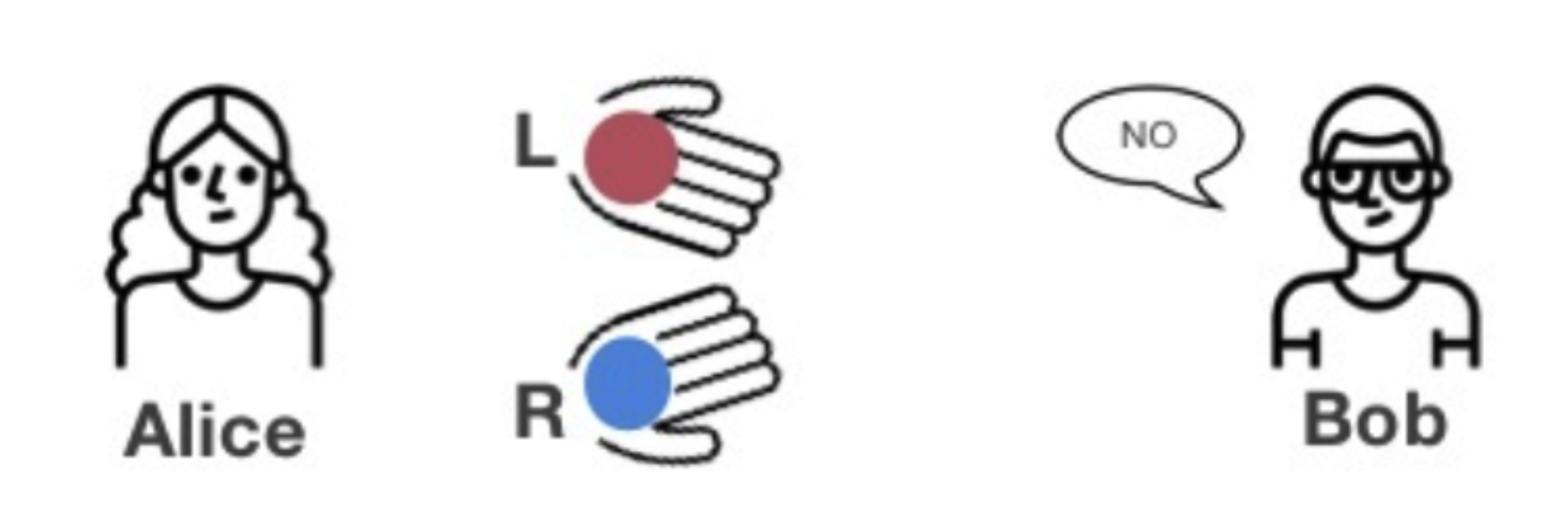
Example 2: Sudoku
The game known as Sudoku requires the player to fill in the remaining spaces on a 9×9 grid with numbers from 1 to 9 so that each row, column, and 3×3 block contains all numbers from 1 to 9 without repetition.
One day, Alice created a challenging Sudoku puzzle for Bob, but after several days of trying, Bob couldn’t solve it and claimed it was an unsolvable puzzle. Alice needs to prove to Bob that there is a solution to the puzzle, but she cannot reveal the correct answer to him.
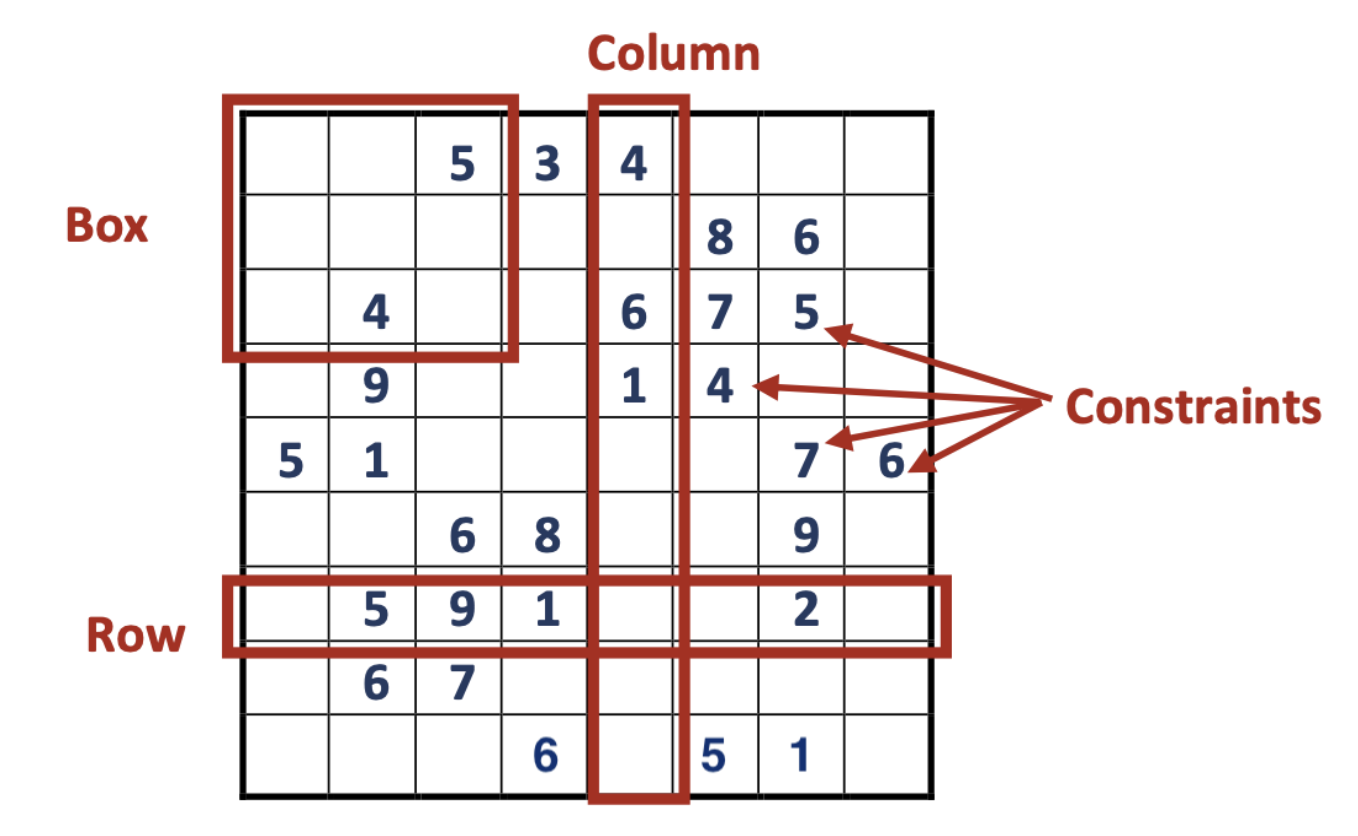
Alice took out 81 cards and arranged them to match the answers to her questions. She placed the answer cards face down and the question cards face up on the table, forming a 9×9 matrix of cards.
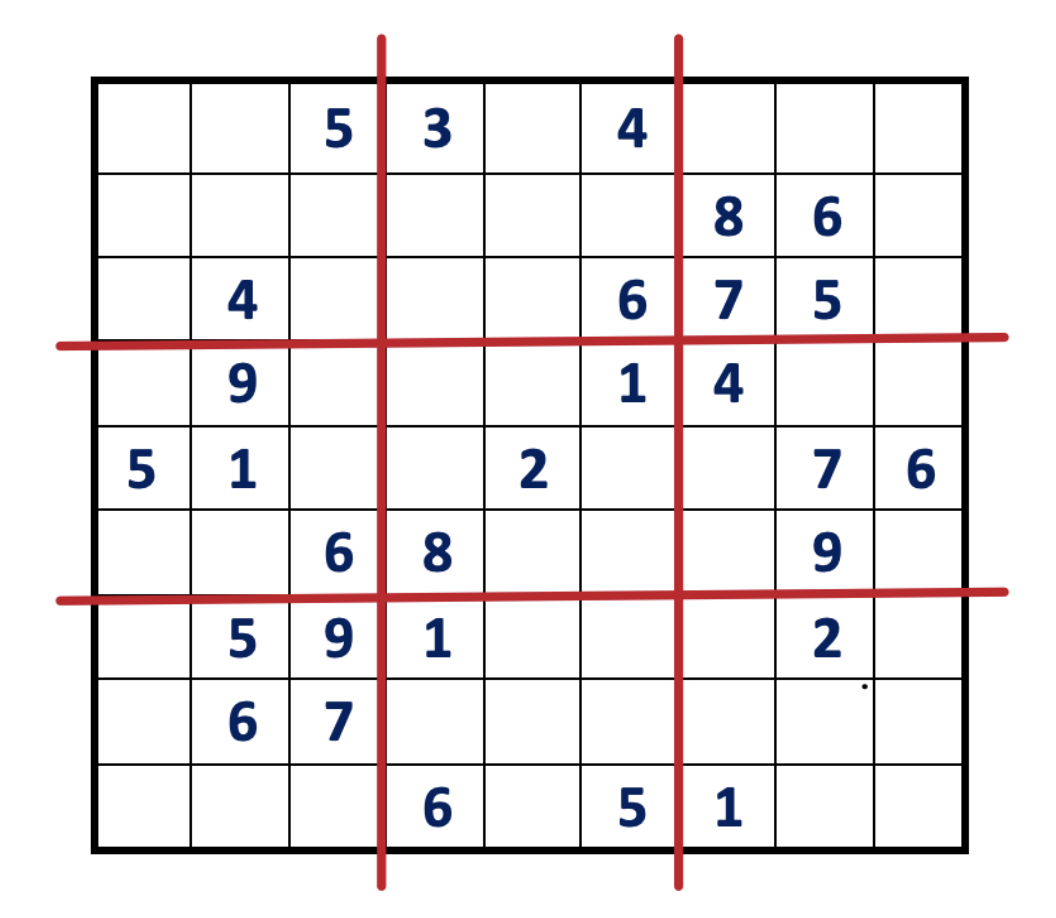
Bob randomly chooses to verify a row, column, or one of the 3×3 blocks. If he chooses a row, Alice places the 81 cards into 9 cloth sacks, one for each row, and shuffles them thoroughly to make sure the cards are mixed.
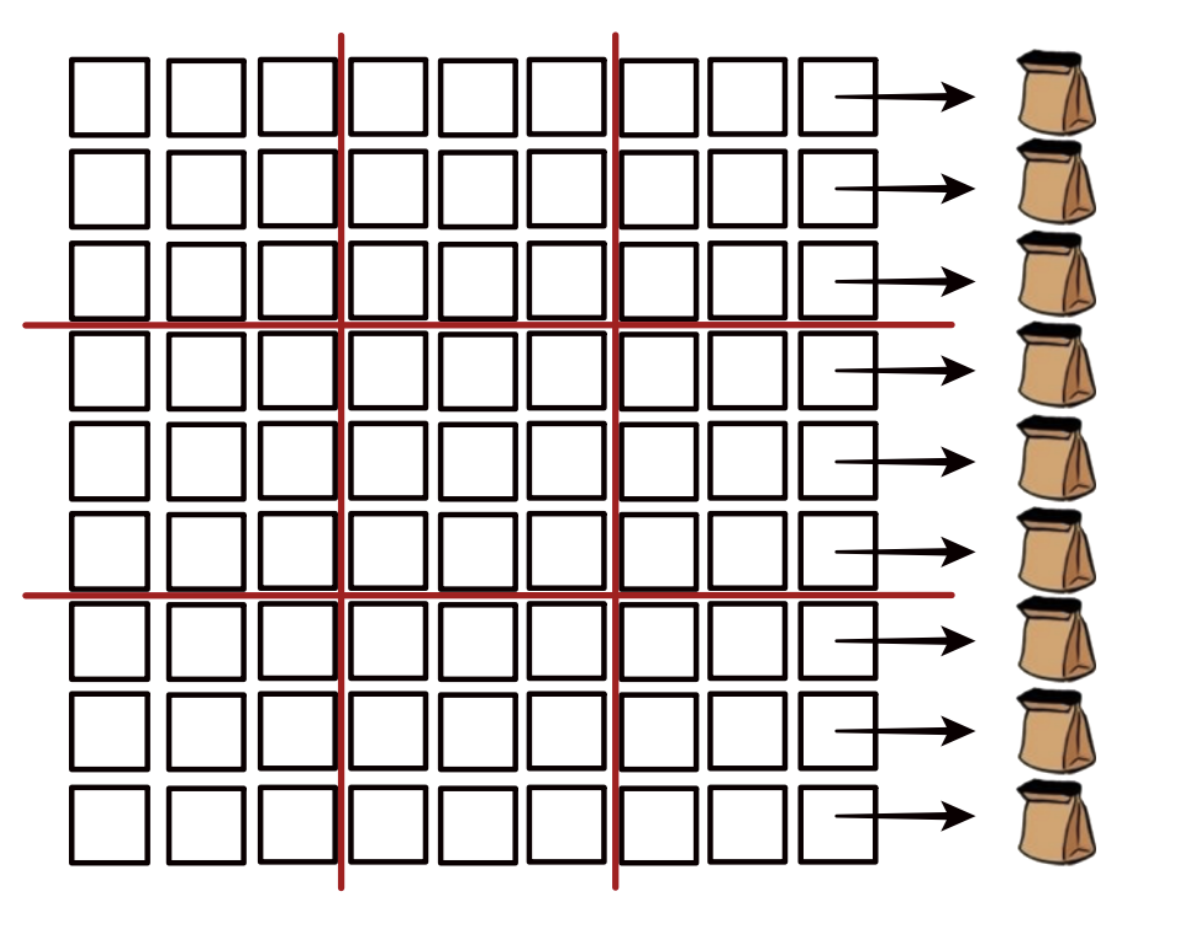
Verify:
In this scenario, since this Sudoku question is part of a public prize challenge, there’s a need to prove to the public that the question has a solution. Alice can’t interact with every member of the public, and if she only interacts with Bob, others might think that Alice and Bob are colluding.
To resolve this issue, an automatic verifier with a trusted setup is required. Alice would only need to submit the cards once, and the machine can automatically repeat the verification based on the initial verification sequence, making the validation process non-interactive. The randomness in this process is not provided by the verifier but by a trusted third party during the initialization stage. This way, the prover can provide the proof directly, and the verifier only needs to verify the proof without any interaction between the two.
Example 3: Tricolor diagram
The four-colour theorem: Any floor plan can be dyed with four colours so that the adjacent areas are of different colours.
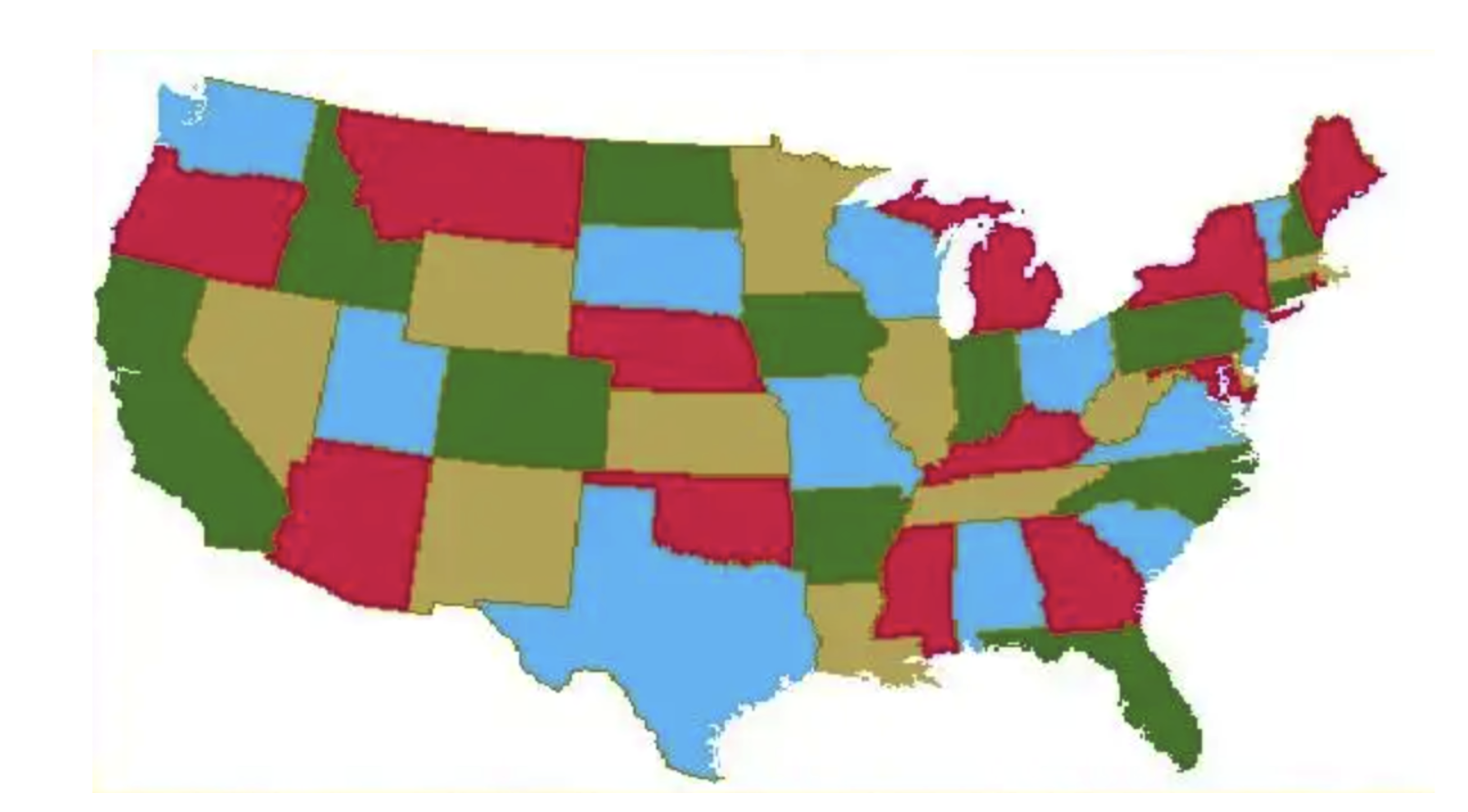
If we use three colors, not every figure is good.
When Bob asks Alice to find the answer to a three-color diagram easily, Alice can prove to Bob that she knows the answer without revealing the coloring scheme by following these steps:
- Alice covers all nodes in the diagram that are correctly colored;
- Bob chooses any two adjacent nodes, and Alice shows him the colors of the two nodes. If the two nodes are different colors, then Bob is 50% sure that Alice truly knows the answer;
- Alice then randomly maps the colors in the current diagram to another color scheme, such as “purple to white, orange to yellow, green to black,” creating a new colored image. Despite the different colors, it is still a valid solution to the original problem. Repeat steps 1-3 N times, and if the two nodes shown each time are different colors, Alice knows that the reliability of her answer is 1-(0.5)^N.
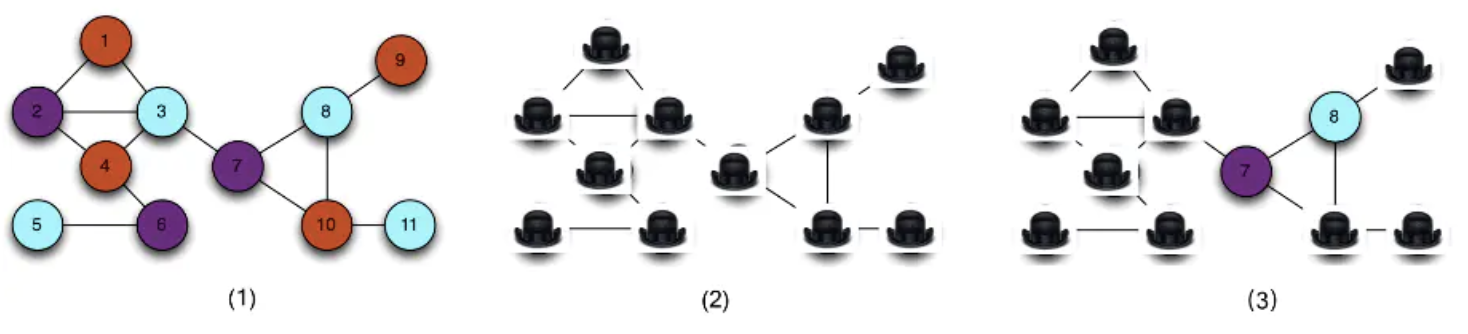
A demo: http://web.mit.edu/~ezyang/Public/graph/svg.html
2. Concept of Zero-Knowledge Proof
Proof System: It is an interactive protocol consisting of two participants, the Prover and the Verifier, and an algorithmic setup. Its purpose is to convince the Verifier of a certain statement. Before the protocol starts, a setup must be performed which takes some common parameters as input and outputs the necessary information for both the Prover and Verifier, denoted as Setup_V and Setup_P respectively. The part of the setup that is shared between Setup_V and Setup_P is called the Common Reference String (CRS) and is commonly referred to as the Trusted Setup.
Setup The time to obtain the setup information depends on the design of the proof system. For instance, the information may be stored on both Prover and Verifier’s hard drives for repeated use or inputted before the protocol begins.
As an example, let’s take the polynomial equation x^2 + 2x + 1 = 9. Alice (Prover) knows the solution to be 2, and Bob (Verifier) needs to be convinced. The statement by the Prover in this proof system would be x = 2 and the Common Reference String (CRS), also known as the Trusted Setup, is x^2 + 2x + 1 = 9. The Setup for Verifier would be multiplication and addition operations, and for Prover, it would be a binary equation solving algorithm.
Nature of Proof System: A proof system must meet the following two properties.
- Completeness: Honest Prover will eventually convince Verifier of the statement. (It really can’t be fake)
- Soundness: Verifier can only be convinced if the statement is true. (Fake can’t be real)
Zero-knowledge: If the Statement is correct, if Verifier cannot derive any other “knowledge” from the interaction other than the correctness of the Statement, Call this system zero-knowledge.
In the example above, x=2 is a piece of knowledge, if Alice can pass x=2 without allowing Bob to deduce x=2. If Bob can verify the statement that Alice knows the solution to this equation, then the proof system is zero-knowledge.
Regarding zero knowledge, there is a strict definition in mathematics, which is probably the following:
If an interactive proof is zero-knowledge, then there exists a simulator with rewind capability that can produce an equivalent distribution of proof copies as when interacting with the real prover. The simulator has no knowledge of the original question but can anticipate the challenge topic and construct a response that is consistent with the probability distribution of the real prover's response, demonstrating the zero-knowledge property of the interaction process.

Non-Interactivity: Proof are only exchanged between the Prover and Verifier in the system. The proof is transmitted as a single message. Non-interactivity offers many advantages and expands the potential applications of the proof system. For instance, in a blockchain system, non-interactive zero-knowledge proof can be attached to transactions, making it possible for anyone to verify them at any time without requiring the transaction author to be online and interact with the validator.
In turn:
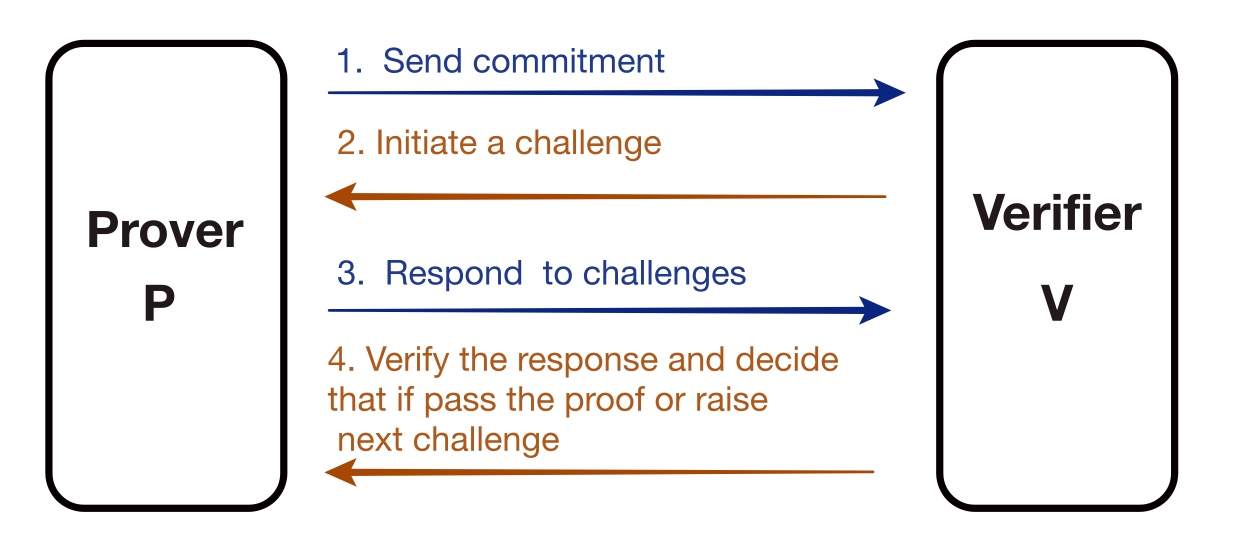
Non-interactive:

The benefits are 1) reduced interaction and 2) public verification
Conciseness: The amount of interaction data of the zero-knowledge protocol < the amount of data interaction of the original proof system.
This article aims to provide a general understanding of zero-knowledge proof and its popular concepts. The goal is for readers to have a basic understanding of zero-knowledge proof. In the next article, we will introduce the basic building blocks of zero-knowledge proof, laying a foundation for a deeper understanding of this topic.
Bibliography
[1] Oded Goldreich , Silvio Micali , Avi Wigderson. Proofs that yield nothing but their validity or all languages in NP have zero-knowledge proof systems. Journal of the ACM. 1991, 38 (3): 690–728.
[2] Shafi Goldwasser, Silvio Micali, Charles Rackoff. The Knowledge Complexity of Interactive Proof System. Siam Journal on Computing, 1989, 18(1):186-208.


